An XBar and R chart – Range chart study is a statistical quality control chart used to monitor variables of product criteria. It may have a drive a subgroup size of two or more to measure standard chart for variables data. Mostly in automotive industry used widely to determine its process stability and predictions.
X bar R chart Uses
In any industry, it may manufacturing, healthcare or service organizations, the stability and consistency in their processes must be monitored from time to time. X-bar and R charts are very popular for providing accurate information on the unit of process shown in the chart. Hence some of the major uses of X-bar and R charts are outlined below in more detail:
To monitor process stability and consistency
Periodically:
Monitoring process averages.
Inspection of a range of processes.
Changes in process.
Improve stability and compatibility etc.
X-bar chart and R chart are required.
Both the X-bar chart and the R chart are actually different, but both are used interchangeably. For example, X-bar charts are used to track the average value of a process, while R charts are used to track the range of a process. So if both are used together it can provide a comprehensive view of the process. It can also be used to identify and control sources of variation.
To identify sources of variation
Naturally, this is an excellent tool for identifying and addressing problems in the process. As can be seen by the X-bar, the mean of the process is changing, while the R chart shows that the range of the process is increasing so that the business can understand what are the sources of variation in the process, so that it is easy to take steps for improvement.
Improving process efficiency
Most units are concerned about waste in their processes. It is obvious that positive process change and continuous improvement are necessary to prevent waste and reduce costs. This improvement is only possible when complete monitoring of the process is available. So that necessary controls and inefficient processes or items can be removed, which eventually turns into an efficient process.
Comparing the performance of different processes or operators
X-bars and R charts can be used to compare the performance of different processes or operators. By comparing process averages and ranges of different processes or operators, it can be identified which processes or operators are performing well and which processes need to be improved.
Finding special cause variances
When we observe X-bars and R chart – Range charts we often notice “outliers data points” – which appear outside the control limits – to understand that the process is out of control, and the process needs improvement.
Determining process capacity
X-bars and R charts can be used to determine process capacity. By comparing the process mean and range with the desired specifications, it is possible to determine whether the process is capable of meeting the desired specifications.
What is the difference between X Bar Chart and R Chart
Although both of these are statistical process control charts, which are used to monitor the stability and consistency of the process from time to time, it is important to understand that they both track processes in different processes.
Here, a detailed table is given which describes the main differences between X-bar chart and R chart:
| X-BAR CHART | R (RANGE)CHART |
|---|---|
| Monitors the average value (mean) of a process over time. | Monitors the range (variability) of a process over time. |
| Plots the mean of a sample of data at different points in time. | Plots the range of a sample of data at different points in time (difference between the largest and smallest value in a sample). |
| Generally, the sample size is between 2 and 10. | Same as X-bar chart, the sample size is typically between 2 and 10. |
| Center line represents the target or desired mean of the process. | Center line represents the average range of the process. |
| Control limits indicate the acceptable range of variation for the process mean. | Control limits indicate the acceptable range of variation for the process range. |
| Used to identify shifts in the process mean | Used to identify changes in the process variability |
| Based on the assumption of normality of the data. | Based on the assumption of normality of the data. |
| Helps to detect and diagnose issues related to process mean. | Helps to detect and diagnose issues related to process range and variability |
X-Bar R Chart Formula
If you want to monitor the mean and range of a process regularly, the control limits for X-bar charts and R charts can be calculated using the following formulas:
X-bar Chart:
Center line (CL) = X̄ (average of the sample means)
Upper control limit (UCL) = CL + A2 * Rbar (A2 is a constant value based on the sample size and represents the distance between the center line and the control limit)
Lower control limit (LCL) = CL – A2 * Rbar
R Chart:
Center line (CL) = R-bar (average of the sample ranges)
Upper control limit (UCL) = D4 * R-bar (D4 is a constant value based on the sample size and represents the distance between the center line and the control limit)
Lower control limit (LCL) = D3 * R-bar (D3 is a constant value based on the sample size and represents the distance between the center line and the control limit)
Remember, control limits are calculated based on the assumption of normality of the data, and it is also important to use appropriate tables of constants to obtain values of A2, D3, and D4 based on sample size. It is also important to mention that these formulas are for standard X-bar and R charts and there are other types of X-bar and R charts that use different formulas.
X-bar and R chart Interpretation
How to interpret X-bar and R charts or how to know through interpretation that processes are in control. It therefore requires an analysis of the plotted points and control limits, and should also include the following points:
- When a chart is created, a limit line or control limit is created. If the plotted points fall within the control limits, it means that the process no and range are stable and consistent, and there are no significant sources of variation.
- Perhaps if the plotted points fall outside the control limits, the process is considered out of control. This means that process means and ranges are not stable and consistent, and may have significant sources of variation.
Pattern
- If the points plotted on the X-bar chart show a clear pattern, such as a trend or cyclical pattern, it may indicate that the trend is changing its meaning.
- It should also be verified that, if the plotted points on the R chart show a clear pattern, such as a trend or cyclical pattern, it indicates that the process series is changing.
- It is worth noting here that, if there are plotted points outside the control limits on both the X-bar chart and the R chart, it may indicate that there is a problem in the process that needs to be addressed.
- If there are plotted points outside the control limits on the X-bar chart, but not on the R chart, it indicates that the process mean is shifting but the range is stable.
- Similarly, if there are plotted points outside the control limits on the R chart but not on the X-bar chart, it indicates that the process range is changing but the mean is stable.
An out-of-control process does not mean that the process is producing bad products, but it does indicate that there is an unknown cause of variation that needs to be addressed, and it is important to identify the cause of the out. Take corrective action to bring the control situation and process back under control.
Initial Process Study
To be conducted for all new or changed products or whenever process change / improvement takes place.
- Measure the identified characteristic as per defined sub group size and frequency (Refer pre-launch control plan ).
- Conduct trial run and note down all the observations as per the study plan. Calculate & plot averages and ranges on the control chart after suitably scaling the charts using format.
- Calculate R bar, X double bar & control limits as per formula given in format and draw lines for them on the chart.
- Analyses the chart & identify actions points on special causes if:
- Any point outside of the control limits
- A run of 7 points all above or all below the control limits
- A run of 7 points up or down.
- Any other obviously non-random pattern.
[Note: R chart should be analyzed first & actions taken accordingly. Then averages chart to be analyzed.]
- Investigate & remove the special causes if any.
- Exclude all subgroups affected by the special causes if any, in both R &X bar charts and recalculate control limits, R bar and X double bar. Confirm that all data points show control when compared to the new limits. Repeat the sequence if necessary.
- Calculate CPK if the process is stable (i.e., no special causes are present) and based on its value, take action accordingly as per PPAP / customer requirements.
Ongoing Process Study
To be conducted for all control plan identified characteristics at defined subgroup size & frequency during in-process inspection.
- Construct X bar & R chart and extend control limits from either initial process study or previous capability study. Divide the control charts into equal three zones namely middle third, upper third & lower third.
- Set up Verification:
- Take samples as per the subgroup size. Calculate average & range and plot the same on the control chart.
- If the results fall in the middle third zone, approve the set up for production.
- If the results fall in outer two thirds, re-set and re-verify till the results fall in the middle third zone.
- Monitor the chart for identifying action points on special causes if any. (Refer I.4 above) and take necessary actions accordingly.
- If there is any shift observed in the process average or range investigate the cause & re calculate control limits if the change is justified.
- Carry out Zone analysis to verify whether more than 2/3rd of data points fall in the middle third of both R chart & X bar chart. (Record the number of points that fall in the middle third & outer 2/3rds on the control chart format & calculate the %).
- If majority of points fall outside the middle zone, investigate the cause & take necessary action.
- Calculate Cpk & verify whether it is equal to or exceeds the current PPAP Cpk value.
- In case of in stability or lesser Cpk, initiate reaction plan as per the Control plan & inform plant manager for taking further action.
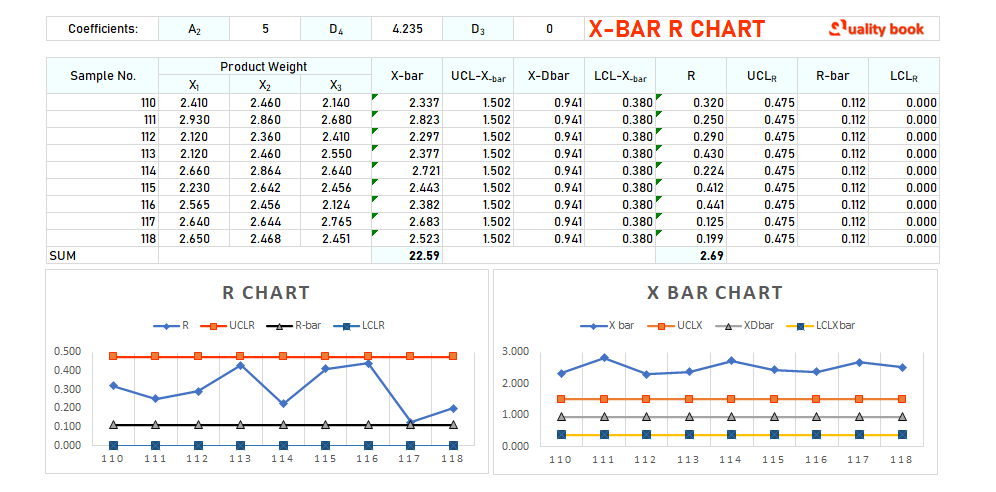
X-Bar and R Chart Solved Example
Here we will take an example, in most of the manufacturing sectors the weight of the product is measured, and in many cases weight is of prime importance, suppose a product comes to be inspected on the basis of weight.
So, suppose a quality inspector takes 10 samples of product every hour, and records their weight. So let’s see how X-bar chart and R chart will be created based on that.
The center line for the X-bar chart is 10.5 (target product weight) and the control limit
Calculated as UCL = 10.5 + 3 * 0.2 = 10.7 and LCL = 10.5 – 3 * 0.2 = 10.3.
The centerline for the R chart is 0.2 (the mean range of sample weights), and
The control limits are calculated as UCL = 0.2 * 2.66 = 0.53 and LCL = 0.2 * 0 = 0.
The plotted points for the X-bar chart fall within the control limits. And there is no clear pattern or trend in the plotted points.
The plotted points for the R chart fall within the control limits. There is no clear pattern or trend in the plotted points.
Based on this analysis, it can be concluded that the process is under control. The process mean (weight) is stable and consistent and falls within an acceptable range. And the process range (variability) is stable and consistent. There are no significant sources of variation in the process.
This is a simple example and a real situation may have other factors to consider and may require further analysis.
This is a solved example, and in a real situation, the information will come from the process being monitored, and the control limits are calculated using the correct tables of constants based on the sample size.